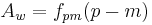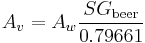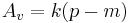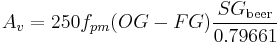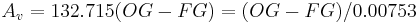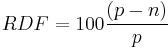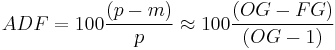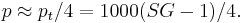Gravity (alcoholic beverage)
Gravity, in the context of fermenting alcoholic beverages, refers to the specific gravity, or relative density compared to water, of the wort or must at various stages in the fermentation. The concept is used in brewing and wine making industry. Specific gravity is measured by a hydrometer, pycnometer or oscillating U-tube electronic meter.
The density of a wort is largely dependent on the sugar content of the wort. During alcohol fermentation, yeast converts sugars into carbon dioxide and alcohol. The decline in the sugar content and the presence of ethanol (which is appreciably less dense than water) drop the density of the wort. The percentage of alcohol can be calculated from the difference between the original gravity (abbreviated OG) of the wort and the current specific gravity (abbreviated SG) of wort. By monitoring the decline in SG over time the brewer obtains information about the health and progress of the fermentation and determines that it is complete when gravity stops declining. If the fermentation is finished, the specific gravity is called the final gravity (abbreviated FG). For example, for a typical strength beer, OG could be 1.050 and FG could be 1.010.
Several different scales have been used for the original gravity. For historical reasons, brewing industry largely uses Plato (°P), which is essentially the same as Brix used by wine industry. For example, OG 1.050 is roughly equivalent to 12°P.
By considering the original gravity, the brewer or vintner obtains an indication as to the probable ultimate alcoholic content of his product. The OE is often referred to as the "size" of the beer and is, in Europe, often printed on the label as Stammwürze or sometimes just as a percent. In the Czech Republic, for example, they speak of "10 degree beers", "12 degree beers" which refers to the gravity in Plato of the wort before the fermentation.
Contents |
Specific gravity
Specific gravity is the ratio of the density of a sample to the density of water. The ratio depends on the temperature and pressure of both the sample and water. The pressure is always considered (in brewing) to be 1 atmosphere (1013.25 hPa) and the temperature is usually 20°C for both sample and water but in some parts of the world different temperatures may be used and there are hydrometers sold calibrated to, for example, 60°F. It is important, where any conversion to °P is involved, that the proper pair of temperatures be used for the conversion table or formula being employed. The current ASBC table is (20°C/20°C) meaning that the density is measured at 20°C and referenced to the density of water at 20°C (0.998203 g/cc). Mathematically
This formula gives the true specific gravity i.e. based on densities. Brewers cannot (unless using a U-tube meter) measure density directly and so must use a hydrometer, whose stem is bathed in air, or pycnometer weighings which are also done in air. Hydrometer readings and the ratio of pycnometer weights are influenced by air (see article Specific Gravity for details) and are called "apparent" readings. True readings are easily obtained from apparent readings by
However, the ASBC table uses apparent specific gravities, so many electronic density meters will produce the correct °P numbers automatically.
Original Gravity (OG); Original Extract (OE)
The Original Gravity is the specific gravity measured before the commencement of fermentation. From it the analyst can compute the Original Extract which is the mass (grams) of sugar in 100 grams of wort (°P) by use of the Plato scale. The symbol  will denote OE in the formulas which follow.
will denote OE in the formulas which follow.
Final Gravity (FG); Apparent Extract (AE)
The Final Gravity is the specific gravity measured at the completion of fermentation. The Apparent Extract, denoted  , is the °P obtained by inserting the FG into the formulas or tables in the Plato article. The use of "apparent" here is not to be confused with the use of that term to describe specific gravity readings which have not been corrected for the effects of air.
, is the °P obtained by inserting the FG into the formulas or tables in the Plato article. The use of "apparent" here is not to be confused with the use of that term to describe specific gravity readings which have not been corrected for the effects of air.
True extract (TE)
The amount of extract which was not converted to yeast biomass, carbon dioxide or ethanol can be estimated by removing the alcohol from beer which has been degassed and clarified by filtration or other means. This is often done a part of a distillation in which the alcohol is collected for quantitative analysis but can also be done by evaporation in a water bath. If the residue is made back up to the original volume of beer which was subject to the evaporation process, the specific gravity of that reconstituted beer measured and converted to Plato using the tables and formulas in the Plato article then the TE is
See the Plato article for details. TE is denoted by the symbol  . This is the number of grams of extract remaining in 100 grams of beer at the completion of fermentation.
. This is the number of grams of extract remaining in 100 grams of beer at the completion of fermentation.
Alcohol content
Knowing the amount of extract in 100 grams of wort before fermentation and the number of grams of extract in 100 grams of beer at its completion, the amount alcohol (in grams) formed during the fermentation can be determined. The formula follows, attributed to Balling[1]
where 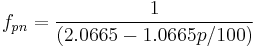 ,gives the number of grams of alcohol per 100 grams of beer i.e. the ABW. Note that the alcohol content depends not only on the diminution of extract
,gives the number of grams of alcohol per 100 grams of beer i.e. the ABW. Note that the alcohol content depends not only on the diminution of extract 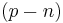 but also on the multiplicative factor
but also on the multiplicative factor 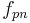 which depends on the OE. De Clerck[2] tabulated Ballings values for
which depends on the OE. De Clerck[2] tabulated Ballings values for 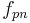 but they can be calculated simply from p
but they can be calculated simply from p
This formula is fine for those who wish to go to the trouble to compute TE (whose real value lies in determining attenuation) which is only a small fraction of brewers. Others want a simpler, quicker route to determining alcoholic strength. This lies in Tabarie's Principle[3] which states that the depression of specific gravity in beer to which ethanol is added is the same as the depression of water to which an equal amount of alcohol (on a w/w basis) has been added. Use of Tabarie's principle lets us calculate the true extract of a beer with apparent extract  as
as
where  is a function that converts SG to °P (see Plato) and
is a function that converts SG to °P (see Plato) and 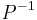 (see Plato) its inverse and
(see Plato) its inverse and 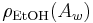 is the density of an aqueous ethanol solution of strength
is the density of an aqueous ethanol solution of strength 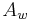 by weight at 20 °C. Inserting this into the alcohol formula the result, after rearrangement, is
by weight at 20 °C. Inserting this into the alcohol formula the result, after rearrangement, is
Which can be solved, albeit iteratively, for 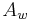 as a function of OE and AE. It is again possible to come up with a relationship of the form
as a function of OE and AE. It is again possible to come up with a relationship of the form
De Clerk also tabulates values for 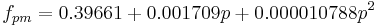 .
.
Most brewers and consumers are used to having alcohol content reported by volume (ABV) rather than weight. Interconversion is simple but the specific gravity of the beer must be known:
This is the number of cc of ethanol in 100 cc of beer.
Because ABV depends on multiplicative factors (one of which depends on the original extract and one on the final) as well as the difference between OE and AE it is impossible to come up with a formula of the form
where  is a simple constant. Because of the near linear relationship between extract and (SG-1) (see specific gravity) in particular because
is a simple constant. Because of the near linear relationship between extract and (SG-1) (see specific gravity) in particular because 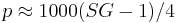 the ABV formula is written as
the ABV formula is written as
If the value given above for 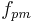 corresponds to an OE of 12°P which is 0.4187, and 1.010 can be taken as a typical FG then this simplifies to
corresponds to an OE of 12°P which is 0.4187, and 1.010 can be taken as a typical FG then this simplifies to
With typical values of 1.050 and 1.010 for, respectively, OG and FG this simplified formula gives an ABV of 5.31% as opposed to 5.23% for the more accurate formula. Formulas for alcohol similar to this last simple one abound in the brewing literature and are very popular among home brewers. Formulas such as this one make it possible to mark hydrometers with "potential alcohol" scales based on the assumption that the FG will be close to 0 which is more likely to be the case in wine making than in brewing and it is to vintners that these are usually sold.
Attenuation
The drop in extract during the fermentation divided by the OE represents the percentage of sugar which has been consumed. The Real Degree of Attenuation (RDF) is based on TE
and the Apparent Degree of Fermentation (ADF) is based on AE
Because of the near linear relationship between (SG-1) and °P specific gravities can be used in the ADF formula as shown.
Brewer's points
Many brewers like to exploit the near linear relationship between (SG -1) and °P to simplify calculations considerably. They define
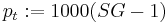 ,
,
call it "points" or "brewer's points" or "excess gravity" and use it as if it were extract. The Plato degree is thus approximately the points divided by 4:
As an example, a wort of SG 1.050 would be said to have 50 points, and have Plato degree of approximately 12.5 °P.
Points can be used in the ADF and RDF formulas. Thus a beer with OG 1.050 which fermented to 1.010 would be said to have attenuated 100*(50 - 10)/50 = 80%. Points can also be used in the SG versions of the alcohol formulas. It is simply necessary to multiply by 1000 as points are 1000 times (SG-1).
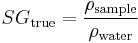
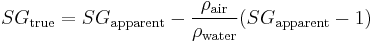
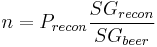
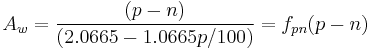
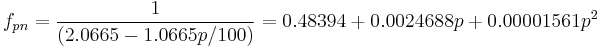
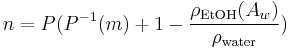
![{\left[p - P\left(P^{-1}(m) %2B 1 - \frac {\rho_\text{EtOH}(A_w)} { \rho_\text{water}}\right)\right] \over (2.0665 - 1.0665p/100)} - A_w = 0](/2012-wikipedia_en_all_nopic_01_2012/I/3da6bd7ff8439b0a8c64ccf47529d6f3.png)